
Table of Contents

OVERVIEW
This chapter provides recommendations for designing interactive learning environments. The type and nature of interactive strategies depend on the underlying learning philosophy. This chapter describes a philosophy of learning, called constructivism, that views learning as individual "constructions" of knowledge. This philosophy and its implications in education are compared to "instructivism," a term used to denote the other cognitive applications to instructional design considered up to this point. In constructivism, the computer is viewed as a source of rich, computational, cognitive tools with which the user can explore and experience many concepts and principles. These learning environments are often referred to as microworlds. Microworlds are compared to both instructional simulations and games. A series of design recommendations based on a merger of instructivist and constructivist philosophies is presented and discussed. A software package called Space Shuttle Commander is presented as one concrete application of these design recommendations.
OBJECTIVES
Comprehension
After reading this chapter, you should be able to:
Application
After reading this chapter, you should be able to:
This chapter continues the discussion begun in the previous chapter of how visualization techniques may contribute to instructional design. This chapter is devoted to the fifth instructional application of graphics first introduced in chapter 2 -- practice. As we will see, the term "practice" may become either insufficient or inappropriate in capturing many of the ideas presented in this chapter. A more general and appropriate term might be "interaction," because the focus is really on how the student participates in and contributes to the learning event. Such interactions within a learning environment would include, but not be limited to, practice strategies. For many instructional technologists, the opportunities for highly interactive learning environments that computers make possible represent the major reason for investing (both economically and intellectually) in computer technology (Hannafin, 1992).
As with the previous chapter, the focus here is on how graphics may contribute to the design of the total instructional system (or learning environment). But this chapter goes much further in stressing the most fundamental issues that influence instructional design. For this reason, this chapter will have, by far, less direct discussions of graphics than any other. Graphics are considered as but one resource for developing interactive learning environments. The goal is not to promote graphics, but to build rich and engaging environments where learners can come in contact with the most intriguing ideas that society has to offer. Graphics offer but one interesting medium with which to "paint this landscape." We might continue this analogy by considering how the human need and talent for artistic expression and inspiration are served by many media -- oil, watercolor, written words, spoken words, stone, marble, clay, etc. -- as well as by many forms -- realistic, impressionistic, surrealistic, functional, natural, etc. Likewise, computer-based graphical techniques offer powerful resources to help fulfill the basic needs of learning and support the talents of instructional design. Throughout this chapter, you are encouraged to consider all instructional media and strategies, but you are also reminded to carefully consider all the graphical ideas and resources discussed so far.
In addressing the issue of instructional interactions, this chapter will present another, completely different, orientation to learning than that presented so far -- constructivism. The concept of constructivism represents a dramatic alternative view to instructional technology. The advice from the previous chapter that instructional designers need to recognize and confront their own philosophical beliefs about learning and instruction becomes even more crucial in this chapter. Again, your interpretation and resolution of these issues will largely depend on this philosophical introspection.
CONSTRUCTIVISM AND ITS IMPLICATIONS FOR INSTRUCTIONAL DESIGN
An historical context may be useful at this point to better understand constructivism and its implications in instructional design. At present, there are two dominant and divergent interpretations of instructional technology, and both envision a significant role for computers in learning and education. The first view is closely aligned with instructional systems development (ISD) and treats instructional applications of computers as related, at least historically, to conventional applications of other educational media. This is the view that has dominated this book thus far. The second interpretation of instructional technology, based on constructivism, considers the computer as a rich source of cognitive tools for learners -- an electronic type of "Play Doh" (Rieber, in press). Let's consider the roots of these two perspectives.
The formal beginning of modern instructional technology is usually traced to the convergence of B. F. Skinner's application of behavioral learning principles to instruction, usually called programmed instruction (PI), and the audiovisual movement of the mid-1900s (see Reiser, 1987, and Saettler, 1990, for detailed historical overviews). Skinner was well-known for creating various teaching machines designed to deliver highly structured instructional treatments to learners. Teaching machines carefully controlled and delivered predetermined reinforcement schedules during instruction -- a skill that Skinner found teachers largely unable to perform. These teaching machines were highly interactive, but also tended to be quite dull and tedious. PI, though generally effective for lower-level learning such as fact learning, was largely inappropriate for higher-level learning. Many current applications of computer-based instruction are really just extensions of the PI paradigm.
Instructional systems development (ISD), as previously defined and discussed, also has its roots in PI. Many PI principles became cornerstones of ISD. For example, the PI principle of objective specification was the precursor to behavioral objectives -- the idea that the required learner response should be determined in advance in precise, observable terms. Empirical testing, the idea that successful lesson components (e.g., appropriate reinforcement, cueing, step size, etc.) could only be determined based on actual field-testing, was the forerunner to formative evaluation (Hannafin & Rieber, 1989a). The PI movement is often criticized today, especially given the popularity (and potential) of the cognitive movement. It is true that PI had serious limitations in covering the breadth of learning outcomes. It is also true that PI conformed to the behaviorist assertion that, essentially, environments control people's behaviors. However, PI remains the first true experiment in seriously attempting to apply learning theory to instructional practice. PI successfully fulfilled the criterion that defines any technology -- the application of basic knowledge for a useful purpose -- and for that reason PI offers many important lessons for future attempts at harnessing other technologies for instructional design.
Cognitive psychology has had a strong influence on ISD in recent years. Cognitive influences have, for the most part, successfully shifted primary attention from the instruction to the learner (Gagné & Glaser, 1987). Cognitive psychology has persuaded instructional technologists to accept the need to consider what happens in between the stimulus and response (i.e., cognitive or mental processing) as the most important part of the learning process, despite the inability to directly observe this process. At first glance, this point may seem trivial and academic -- stuff that makes for good discussions in graduate school classes and nothing else. In actuality, this is a significant turning point for the field and is especially relevant for instructional designers. Cognitive models, such as the information-processing model introduced in chapter 4 (see Figure 4.1), have become the focus of instructional design. Cognitive concepts, such as mental encoding and retrieving, depth of processing, metacognition, and so on, have expanded the range of instructional ideas and have opened up new approaches for identifying and solving instructional problems.
Despite the positive influence of cognitive psychology on instructional design, the skill, task, and procedural aspects of "the model" are still largely retained. As discussed in the last chapter, instructional design is still largely based on achieving the learning objectives identified early in the process. Thus, in general, the goal of any one instructional design is to bring the learner to the point of mastering the learning objectives as efficiently and as effectively as possible. Certainly, a learner's prior knowledge, abilities or aptitudes, needs, and interests have a major influence on how the instruction is designed. However, most of the major instructional decisions, such as how content is selected, sequenced, structured, and presented is usually made on behalf of the learner. Some use the term "neo-behavioral" to define this "mingling" of behavioral and cognitive philosophies (Case & Bereiter, 1984).
The term "practice" is most appropriate in this first interpretation of instructional technology because it describes the interaction as per the events of instruction. By following presentation strategies with practice, the lesson information completes, in a sense, a cycle or "round trip" between the instructional materials and the learners -- the instruction elicits a response from the learners, followed by the instruction providing the learners with appropriate informational feedback about their performance. Practice is viewed as but one part of an instructional system, and, therefore, its purpose is to complement the other instructional components (i.e., orientation strategies, presentation strategies, testing, and strategies to enhance retention and transfer).
Given the dominant role that instruction continues to play in this type of learning environment, we might coin our own "-ism" word by using the term "instructivism" to describe this interpretation of instructional technology (Rieber, 1992, in press). Instructivist models characterize learning as a progression of stages starting at the novice or beginner level in a particular domain and ending at the point where the learner becomes an expert. This characterization is similar to Gagné's concept of a learning hierarchy where lower-level learning is considered prerequisite to higher-level learning. All instructivists make the assumption that one purpose of instruction or education is to help the learner understand the "real world." Another assumption is that one group of people, such as teachers and other educators, have the authority and responsibility to make decisions about what should be taught and how it should be taught to another group of people, such as students. Of course, this means that one assumes that there is one objective interpretation of the world to be recognized and accepted and that certain pieces of this world knowledge are important enough for everyone in the society to learn. As we are about to see, not all educators share these views or assumptions.
The second interpretation of instructional technology is patterned after a philosophy of human learning and cognition known as constructivism (Jonassen, 1991a). Constructivists consider the major goal of education to be the creation of a rich assortment of cognitive tools that are made available to learners to help them explore their environments. It is then up to learners to decide for themselves what is real or true. Constructivists usually define instructional technology as the generation of computer-based tools that provide rich and engaging environments for learners to explore. These environments are frequently referred to by constructivists as microworlds (an idea we will revisit in depth later in this chapter) because they allow learners to participate in a set of ideas until they begin to "live" the ideas, not just study them (Dede, 1987; Papert, 1980, 1981). The next section will provide a brief overview of some of the main tenets of constructivism as they apply to learning and instruction.
Constructivism: An Overview
There is a story that someone once commented to philosopher Ludwig Wittgenstein that people living in medieval Europe before the time of Copernicus must have been pretty stupid to have believed that the sun actually circled the Earth and that common sense should have told them the opposite was true. Wittgenstein is said to have agreed, but also wondered what it would have looked like if the sun had been circling the Earth -- the point being that it would have looked exactly the same to most people (Burke, 1985). The idea that the Earth was at the center of the universe was just as true to these people as the concept that the Earth orbits the sun is to us. Information does not become knowledge just by its telling.
It is tempting to believe that we, living today, somehow know the real truth about the world, that we are somehow better informed than those poor, ignorant folks who lived many years ago. Ours is the real science, right? But before you answer this question, you need to examine your beliefs, even those of supposedly objective truths from mathematics and science. How do you really know that the Earth goes around the sun? Just as Wittgenstein observed, our perceptions tell us something very different, yet we have come to accept another fact as being true and our perceptions as being false. All too often, we teach people something as being true without considering what this really means at the individual level. Much education is involved in telling people what to believe. However, true understanding cannot be imposed on someone, but instead must come about by a personal revelation (Bruner, 1990).
Actually, science offers some stunning historical examples of how differences in interpreting the world actually meant that the world was a different place to people. It all depended on one's point of view. Consider the idea above, proposed first by Aristotle, that the Earth is at the center of the universe and is unchanging. If you do not believe that the Earth changes, then you do not look for changes. Our view of science as discovering and exploring the heretofore unknown does not exist in such a world. Compare this to a Newtonian world, where the Earth circles the sun in an elliptic orbit according to certain laws of nature. Aristotle's ideas are just plain wrong in Newton's world. For hundreds of years, Newtonian physics represented the truth of the physical world. The role of science was to gather more information and search for other laws of nature -- a view that persists today. But in Einstein's world of curved space and black holes, Newton's laws do not seem to be enforceable -- even the behaviors of time and light can change (Hawking, 1988). If Newton is wrong, then maybe so is Einstein. Perhaps the universe really is just a grain of sand on some cosmic beach.
Constructivists believe that each of us defines the world (and ourselves) by what we know and believe (Goodman, 1984; Watzlawick, 1984). Each person perceives and interprets the world in a unique way. Instead of suggesting that knowledge can be transferred from one person to another, information from the environment is used as building blocks for individuals to construct knowledge. This construction process is believed to be a natural consequence of meaningful interaction with one's environment or culture. One's knowledge is never static, but dynamic and ever-changing.
But what constitutes meaningful interaction? Consider Newton's first law that states that an object at rest remains at rest and one in motion remains in motion unless acted on by some outside force. Compare two very different instructional designs for teaching this principle. First, consider a physics class where a teacher lectures about the principle to a roomful of students sitting attentively in their chairs, followed by a series of homework problems from the textbook. Next, consider a second classroom where the teacher has each student build and test a series of ramps with a variety of objects (in order to test different levels of friction). The first scenario has students interacting with information selected and interpreted by someone else. In the second scenario, students begin by interacting with the principle itself. The teacher's job is to facilitate, manage, or at times, guide, the students' interactions.
Is Newton's first law for real, or are there a series of general conclusions based on shared experiences that people can resolve among themselves? With help from the teacher, the group may form some consensus about Newton's first law, but the truth of the law rests within each individual. Interestingly, there is research indicating that physics students who learn physics given instruction similar to the first scenario can pass tests, but may actually revert to their personal view, or theory, of the world when confronted with novel physics problems to solve (Eylon & Linn, 1988). Students may know how to compute the formulas, but their conceptual understanding may not have been changed. See Box 8.1 for a follow-up discussion on this second instructional scenario using the physics of baseball.
Constructivists believe that learning is enhanced in environments that provide a rich and varied source of engaging experiences (Papert, 1988). Computer enthusiasts feel that the computer offers a powerful medium for exploring and discovering many ideas, just as a young child might explore the concepts of volume with a sandbox and mass and momentum with marbles. The computer's ability to present graphical representations is usually considered one of its most important attributes. In constructivism, quality of knowledge structures, not their quantity, is the issue. In other words, learning is not about acquiring new knowledge, but the constant reconstruction of what someone already knows (Forman & Pufall, 1988a; Fosnot, 1989). As a person's knowledge structures are continually "revised," there is the occasion where a new structure is formed because new information just no longer matches the available structures. As Forman and Pufall (1988b) note: "Central to constructivism is the assumption that to know is to continually reconstruct, to move from a more to a less intuitive state" (p. 240). The cognitive theories of Jean Piaget still provide among the best accounts of the constructivist view in education.
|
|
|
Having been born and raised on the Southside of Pittsburgh, I grew up surrounded by baseball stories. People there sometimes debate who had the best throwing arm of all time. My own personal choice is Roberto Clemente. Clemente played right field for the Pittsburgh Pirates until his tragic death in a plane crash on New Year's Eve, 1972. According to one account, which may be perhaps more legend than fact (though I have chosen to believe it), is that at old Forbes Field he once threw a baseball over 400 feet -- on a fly -- just in time to tag out the base runner sliding in at home plate. How far can you throw a baseball? One hundred feet? Two hundred? Three? How about a mile? "Whoa!" you say, "I have a major league arm, but it isn't bionic!" The point is that no matter how far you think you can throw, you know that eventually the ball is going to come to a stop. Find the highest hill or wait for the strongest wind before you toss it but the outcome will inevitably be the same -- the ball will come to a dead stop. Little wonder that Aristotle thought that the "natural" state of an object was at rest. Objects seem to "seek" or "prefer" to be at rest. However, Isaac Newton said otherwise. His first law of motion states that "every body persists in its state of rest or of uniform motion in a straight line unless it is compelled to change that state by forces impressed on it." In other words, an object at rest will stay at rest (overlapping with Aristotle), and an object in motion will continue in motion (so much for Aristotle), unless something else comes into the picture. But all our everyday experiences lend far more support to Aristotle than Newton. So why do we believe (and teach) Newtonian, rather than Aristotelian, physics in our schools? Perhaps a better question is do we really believe Newton? In fact, most of the credit for Newton's first law really belongs to Galileo (Newton was born the year in which Galileo died). Galileo proved to himself that Aristotle was wrong by the following set of experiments. Place a wooden block on a perfectly horizontal surface. Give the block a push and watch it slide a short distance until it stops. Now repeat the experiment over and over with smoother and smoother blocks and surfaces. Assuming that you keep giving the block the same size push each time, you will notice that the block goes a little further each time the smoothness of either the block or the surface is increased. Now try the experiment with a ball instead of the block. Again, the distance traveled is increased (be sure to keep the size of the push the same each time). You have probably figured out by now that we are simply reducing the amount of friction that is being exerted against the object. A ball rolling across a frozen lake or a golf ball hit on the moon will go a long way before stopping because of the same principle (although both will eventually stop). Although Galileo could not eliminate friction completely, he extrapolated his findings to a "what if we removed all the friction" situation and concluded that the object would move forever in a straight line. So how far could you throw a ball if all other forces, such as gravity and friction, were removed? According to Galileo or Newton, even the weakest toss would make the ball go forever. Do you believe this, I mean, really believe this? Maybe you need to prove it to yourself. Just don't throw the ball near the speed of light, then the rules change. |
Influence of the Work of Jean Piaget
Educational applications of constructivism are closely associated with the learning theories of Jean Piaget (Vuyk, 1981). Although the brief account that follows may appear to many as a caricature of Piaget's theory, it should help in understanding and applying constructivism to the discussion of educational implications in later sections.
Piaget's theories can be classified in two ways -- stage-dependent and stage-independent (Mayer, 1983). Most of the attention is usually given to Piaget's stage-dependent theory, which suggests that there are four stages of cognitive development that people supposedly progress through (at least potentially) in their lives -- sensorimotor, preoperational, concrete operations, and formal operations. However, our attention will be devoted to the Piaget's stage-independent theory.
Piaget's stage-independent theory concerns two assumptions about how internal mental structures are formed (Piaget, 1952, 1970). The first is the need for adaptation, or the ability of an individual to survive and prosper given an ever-changing environment. The second is organization, which is one's need or desire for a stable or coherent world. These two processes create an internal or intrinsic conflict for people. The goals or needs of one process directly contrast those of the other. Lifelong learning requires a constant balancing between the two. Just as one struggles to achieve an organized world, the environment presents a new situation or problem. Piaget defined a process, called equilibration, that explains how people accomplish this balancing act. Equilibration consists of two mechanisms: assimilation and accommodation. New information from the environment is assimilated, or subsumed (or understood), under an already existing mental structure. For example, a baby who has learned to throw a tennis ball is just as likely to throw an orange or an apple the first time each is encountered. Accommodation, on the other hand, describes the process where the child builds new structures from the existing structures when the new information no longer fits. Thus, the baby soon learns that some round objects are meant to be thrown, but others are to be eaten.
Life's everyday encounters with the environment inevitably lead to one natural conflict after another, conflicts that are resolved by assimilation and accommodation. Interestingly, learning can only occur when an individual is in a state of disequilibrium, also known as cognitive conflict. When confronted with new information from the environment, a person naturally seeks to assimilate, or incorporate, this information into structures that already exist. The process of accommodation is triggered when new information no longer fits or matches the existing structures, necessitating the formation of new structures. According to Piaget, this process never ends, though the range or breadth of potential new structures that can be formed are linked to the developmental stage of the individual. But that is another story.
Educational interpretations of constructivism consist of three properties that are closely aligned with Piaget's theories: epistemic conflict, self-reflection, and self-regulation (Forman & Pufall, 1988b).
Epistemic conflict is really just the Piagetian process of equilibration described above. Learning is a result of trying to resolve a problem encountered in the environment that is outside the person's repertoire. Of course, the conflict may have been artificially induced, such as a problem presented by a teacher, but resolution of the problem can only be achieved by the individual. In the constructivist vernacular, each resolution is a construction. Just because the environment has posed a problem or conflict does not mean that the individual will choose to pursue resolution. If the problem is perceived as too easy or trivial, then the individual will not find the problem worth pursuing. If the problem is too difficult, the individual may simply choose to ignore it.
The property of self-reflection involves an individual's deliberate attempt at objectively and explicitly representing reality in response to a conflict. Arriving at a resolution or solution to the conflict involves the property of self-regulation. Cognitive structures are spontaneously restructured according to the mechanism of assimilation and accommodation. Old mental structures become more refined or comprehensive. New mental structures are formed. Once conflict and reflection trigger self-regulation, the individual acts until resolution is attained, either by explaining the new information as another, extended example of something that was already known (assimilation), or by the formation of something new (accommodation).
Microworlds
What does all of this have to do with instructional design? If one accepts the constructivist notion that knowledge is not transferred from one source to another -- such as from instruction to the individual -- but is personally constructed as a result of cognitive conflicts with the environment, then "instruction" is really a misnomer because individuals teach themselves. However, we will use the term "instruction" to describe the deliberate attempt to structure the environment in such a way so as to foster, nurture, or trigger the equilibration process in an area of inquiry believed relevant. Constructivists usually use the term microworld to describe placing learners in contact with such learning environments (Papert, 1980; Dede, 1987). Table 8.1 lists some characteristics of microworlds, as defined and explained in the sections to follow.
| TABLE 8.1 Characteristics of a microworld |
|
Probably the most well-known computer-based application of constructivism is LOGO, a computer language that reflects and promotes Piagetian learning. LOGO was the result of a collaborative effort between the Massachusetts Institute of Technology, and Bolt, Beranek, and Newman, and was initially funded by the National Science Foundation. Many people contributed to LOGO's development, including Wally Feurzeig, Daniel Bobrow, Hal Abelson, and Andy diSessa. However, Seymour Papert is usually credited as LOGO's chief developer and spokesperson. LOGO lets learners explore many areas, including mathematics, science, and metacognition (thinking about thinking), by placing them in contact with a microworld in which these concepts are represented. A microworld, as the name suggests, is a small, but complete subset of reality to which one can go to learn about a specific domain. Personal discovery and exploration are essential ingredients of learning in a microworld (Dede, 1987; Papert, 1981).
Microworlds are among the most promising attempts at creating computer environments that foster an individual's construction (assimilation and accommodation) of knowledge. Microworlds, though a constructivist invention, offer instructional designers two key advantages. First, microworlds present learners with experiences within specific boundaries of a domain. Second, microworlds offer learners "stepping stones" between interconnected ideas within the domain by allowing rudimentary ideas to first become established and then transformed into more sophisticated aspects of the domain.
Turtle geometry, as defined and discussed in chapter 3, is one such LOGO microworld that gives learners access to geometric principles through interactive graphics (Abelson & diSessa, 1981; Lockard, Abrams, & Many, 1990; and Lukas & Lukas, 1986). Students "drive" the turtle, which leaves a trail as it goes around the screen. The turtle commands, known as primitives, express fundamental geometric ideas of space and distance. As alluded to in chapter 3, the purpose of turtle graphics is not to produce graphics, but to use graphics as the key for experiencing a set of powerful ideas that, in turn, leads to learning about mathematics and science. The rest of this section elaborates on these powerful ideas.
Successful LOGO learning experiences are founded on several key ideas, many associated with programming. For example, LOGO is a procedural language that encourages top-down problem solving in which a large problem can be broken down into more manageable chunks. Students can increase the turtle's vocabulary by creating new commands, or procedures. The definitions of new turtle procedures consist of LOGO primitives, as well as procedures created earlier.
However, the turtle geometry microworld best represents a constructivistic learning environment by the turtle simply being a good "object to think with" (Papert, 1980). At the heart of constructivism is a search for other good objects that learners can use to construct knowledge. Almost anything can become a good object to think with: pots, pans, mud pies, blocks, Legos, etc. Some are more flexible and generalizable to a variety of domains than others. Meaningful interaction with objects in the environment liberates and encourages the equilibrium process.
The turtle is but one example of an object to think with that is made possible through computer-based visualization. Papert contends that the computational and graphical power of the turtle makes accessible to children certain ideas from the world of mathematics and problem solving that previously were considered too formal or abstract for young learners. Two characteristics of the turtle help make this possible: the turtle as a transitional object, and the turtle as an aid to debugging. Both characteristics offer many lessons to other would-be microworld designers.
It is common for young children to begin using LOGO for self-guided learning within minutes of encountering the turtle. This is believed to be achieved by the role of the turtle as a transitional object between the children and the computer. The turtle is body syntonic with the child in that both share two important characteristics -- a position and a heading. This simple fact has powerful learning consequences. From the start, even a young child has something in common with the turtle. This commonality immediately provides the bridge to new ideas. Papert contends that young children quickly anthropomorphize the turtle (giving it human characteristics), thus creating an ego syntonic relationship with the turtle. This encourages the Piagetian concept of decentering, in which young children begin to interpret the world from several perspectives. The anthropomorphization of the turtle also gives children a way to express mathematical ideas. Children begin to acquire the vocabulary of turtle geometry through their communications with the turtle. Since the language of the turtle is LOGO and the language of LOGO is mathematics, LOGO gives children a means to verbalize mathematics (Papert, 1980).
The second important characteristic of the turtle is as an aid to debugging, or the identification and correction of errors within a computer program. Whereas errors are something to be avoided in most forms of instruction, constructivists prefer the idea that errors are a natural consequence of interactions with the environment. Instead of being negative, errors are useful so long as they provide a rich source of information to help guide subsequent interactions. Successful error handling drives the way in which an individual adapts to meet other challenges from the environment. The informational feedback that errors provide is very potent, especially when a learner has a strong commitment to the action that triggered the error. Error detection is made intuitively obvious in LOGO with the turtle's role as a graphical tool. The turtle's animated graphics provide instantaneous graphic feedback. This rapid exchange between the learner and computer in the form of learner action/intention and animated feedback encourages risk-taking and hypothesis-testing. The forming and testing of hypotheses based on animated graphical feedback can be a powerful learning strategy.
Papert (1980) suggests that microworlds, like all powerful ideas, should fulfill four criteria: they should be simple, general, useful, and syntonic. Syntonic learning, which loosely translates as "it goes together with," in a sense subsumes the other three criteria. Syntonic learning involves connecting new ideas to prior knowledge and engaging the learner in a never-ending pattern of going from the "known to the unknown." Constructivists say learner control is essential in microworlds, a point that contrasts with research on learner control of direct instruction that suggests that learners are often poor judges of their own learning paths (Clark, 1982; Steinberg, 1977, 1989).
Learning within a microworld relies on a learner's natural tendency to seek equilibrium. Successful microworlds actually encourage learning conflicts in order to activate the process of equilibration, since it is believed that only through the resolution of these conflicts can learning take place. The trick is to structure the microworld so that learners have an environment in which conflict resolution is within their grasp. It is this purposeful structuring by the microworld designer that offers a link with instructional design and the other issues discussed so far in this book. Microworlds offer learners an opportunity to exercise a cognitive or intellectual skill that they would be unable or unlikely to do so on their own, either because there is no intrinsic reason to do so or because no sufficient tool is available with which to allow them to begin the experience.
THEORY INTO PRACTICE: BLENDING CONSTRUCTIVISM WITH INSTRUCTIONAL DESIGN
Although many principles of constructivism offer much potential in developing successful learning environments, it is usually difficult for people to see practical examples, given the typical constraints found in most schools and training situations. Indeed, any form of instruction, that is, some form of structured learning experience, is totally outside of extreme interpretations of constructivism. In other words, radical constructivism translates into instructional chaos. I feel that a compromise between the instructivist and constructivist "camps" can be reached. As a start, the next section will discuss several areas of research and development that complement the design of microworlds.
Mental Models
Mental model research closely parallels microworld design. Everyday activities require us to interact with a complex environment. It has been suggested that people form mental models of the physical world (see Gentner & Stevens, 1983, for a review). A mental model is simply an individual's conceptualization, or theory, of a specific domain or system. The purpose of mental model research is to lay out as precisely as possible how people understand a certain domain.
Students develop and use mental models to help explain and solve general classes of problems. Similar to the Piagetian idea of a mental structure, mental models are loosely organized and forever changing as new interactions with the environment suggest adaptations. So far, mental model research has focused on technical domains, like physics or electricity, simply because they are far more normative and are more easily made explicit than most other domains, such as parenting. Despite the use of such highly specific domains, theorists suggest that people form mental models of a large number of systems ranging from the kitchen stove to Newtonian mechanics (revisit Box 7.2 from chapter 7 for a discussion of ways in which people form mental models of everyday things).
Mental models serve us with both explanatory and predictive skills. Survival demands that we are able to predict everyday events with a high degree of success. The routine need to cross a street is a good example. Beyond all of the perceptual requirements (such as estimating the width of the street and the speed of oncoming cars) is a need to understand the many "street systems" that operate together. Just a few of these systems include the workings of automobiles, traffic lights, and physics. Our understanding of each system is crucial as we decide when is an appropriate time to cross the street as well as if we can casually stroll across or should attempt an Olympic sprint. Any misunderstanding of one of these systems could be as deadly as any misjudgment of distance or speed. For example, consider your mental model of an electric "walk" sign at an intersection and what it means when it begins to flash. Can you still initiate the crossing? What should you do if you're already part way across? Obviously, each interpretation can have dramatically different consequences. Mental models of everyday things usually form through interactions with the environment. However some systems, such as the physical sciences, are difficult to understand through a wide range of random interactions. Microworlds may offer a platform for people to accurately understand any number of systems.
The application of mental models to the instructional design of microworlds involves considering three things: the target system, the user's mental model of the target system, and the building of a conceptual model of the target system (Norman, 1983). The target system is the actual system that a learner is trying to understand. Newtonian mechanics, thermodynamics, or even a refrigerator can be examples of target systems. A user's mental model describes his or her personal understanding or theory of the target system. People use their mental models to describe and predict how the target system works. Of course, a user's mental model may not be an accurate reflection of the target system. Consider your understanding of how your home's thermostat controls the furnace. Does setting the thermostat to 90 degrees warm a chilled room any faster than setting it to 80 degrees? If you hold the valve theory, you would answer yes. This mental model is based on the idea that the thermostat controls a valve that lets more heat into the room. If you hold the timer theory, you would answer no because this theory states that when the furnace is activated, it always puts out the same amount of heat. The thermostat simply signals the furnace to turn itself off when the desired temperature is reached (Norman, 1988). Does pressing the already-lit elevator button in the lobby help ensure that the elevator will really come? Does repeated pressing of the button make the elevator come to your floor faster? Your actions are a result of your mental model for elevators (though some may also be rooted in superstitious behavior).
To help users more accurately understand a system (and subsequently to alter their mental models), a conceptual model may be designed and presented to them. Conceptual models act as both bridges between the target system and a user's model and anchors upon which a user's model can grow and develop (Mayer, 1989). Conceptual models are usually invented by teachers, designers, or engineers. A microworld is largely synonymous with an interactive conceptual model. It embodies the simplest working model of a system in which an individual can begin to understand the target system. A conceptual model can often be metaphorical to the target system, such as suggesting that a computer system is like a "desktop." In such cases, conceptual models, like microworlds, offer a temporary doorway to a set of larger ideas. For example, Papert (1980) has recounted the way in which his fascination with gears as a young boy offered him a beginning conceptual model of mathematical ratios and proportions. For Papert, gears became a personal microworld that helped make the many abstract mathematical ideas more concrete for him.
In order for an interactive conceptual model to truly become a microworld, one more condition must be met -- students must find the experience personally satisfying and rewarding. Designing a microworld in such a way so that students choose to engage in the activity involves the issue of intrinsic motivation, which was first defined and described in chapter 4. Lawler (1982) has suggested that microworlds, like those presented in LOGO, are successful because they produce "neat phenomena," or "phenomena that are inherently interesting to observe and interact with" (p. 141). However, constructivists offer little guidance on this issue to designers of microworlds. Turtle geometry, for example, may capture an innate human interest in the visual appeal of graphics.
Activities that are intrinsically motivating rely on student-centered incentives, rather than external lesson reinforcement. We will revisit the topic of intrinsic motivation in a later section of this chapter using a context that offers many similarities to microworlds -- computer games. But first, we will consider an instructional format that offers the most similarities to microworlds -- simulations.
Simulations and Their Relationship to Microworlds
When an instructional designer first hears a description of a microworld, the first reaction is usually to confuse it with a simulation. While characteristics of the two can heavily overlap, each can remain mutually exclusive. It all depends on design and, most important, how they are used in a learning environment. A microworld has two essential characteristics that distinguish it from a simulation. First, a microworld holds the simplest model of a system or domain that is still recognizable by an expert in that domain. Second, the parameters of a microworld are carefully designed to match the level, experience, and interest of the learner. This second characteristic is the most important because it offers the user an entry point into the domain.
In contrast, a simulation is any attempt to mimic in some form a real or imaginary environment or system. Simulations have a long history in education. Box 8.2 describes the most recent "sibling" to simulations, most commonly called virtual reality, that uses the most sophisticated visualization techniques available (Rheingold, 1991). Conceptually, virtual reality systems "transport" the user from one reality to another so that what seems to be present really is not. An essential characteristic of any simulation is that there is a set of rules or model upon which the simulation is based (Willis, Hovey, & Hovey, 1987). Simulations serve two purposes. The first is to provide a means of studying a particular system, such as a scientific simulation. For example, a meteorologist may design a simulation of a tornado in order to better understand the conditions under which tornadoes form. An economist might construct a simulation of a free-market economy to understand the effects of government regulation. In both cases, the simulation would necessarily be based on some theory of the system. In other words, the simulation seeks to model theory. In this way, scientists can test and revise their theories of complex phenomena, because direct experience is either impossible, expensive, or dangerous.
The second purpose of simulations is educational -- to teach someone about the system (Reigeluth & Schwartz, 1989). As with scientific simulations, educational simulations are used because there is some inherent reason not to have users experience the system directly. Typical reasons include cost, danger, and inaccessibility. Students learn about the system by observing the results of their actions or decisions through feedback generated by the simulation (Duchastel, 1990-1991). Computer simulations usually offer the advantage of providing the feedback to the student in real-time since the mathematical model of the system is programmed into the computer. Additionally, the computer can be programmed to speed up or slow down the process, a technique that is especially useful if the real system either occurs too fast (e.g., an internal combustion engine) or too slow (e.g., deforestation) for feedback to have any meaning.
Alessi and Trollip (1985) further distinguish simulations on the nature of their interactivity. Some types of simulations, similar to the scientific simulations described above, allow the user to choose or set the value of variables (such as the amount of gravity) and then watch the effects of their choices (such as how much time it takes an object to fall). Other simulations, such as the operation of a complex piece of machinery, give the user chances to learn the operating procedures without the risks and costs associated with its real use.
It is common for simulations to be visually based, although visuals are not an inherent characteristic of a simulation. Visuals may be used in order to provide greater similarity between the simulation and the actual system (e.g., a realistic visual of a cockpit and changing landscape for a flight simulation) (Alessi, 1988). It is hard to imagine an educational simulation without visuals, yet this is simply a design decision. The economics simulation described above might simply use a spreadsheet's row and column design to test a series of "what if" scenarios with the raw data over time. The visual design of a simulation's interface is probably best approached in terms of how the visuals provide natural mapping between the users' execution and evaluation of intended actions while they are participating in the simulation (see chapter 7 for a discussion of this concept).
|
|
|
Simulations allow users to experience and participate in an environment that models some real (or imaginary) system. Simulations provide experiences in a context that is hoped to closely resemble the system that is being simulated. Simulations are often used because there is a reason why the system cannot be experience for real, such as time, cost, risk, complexity, or unavailability. However, every simulation places the user at a distance from the system being modeled. There is no mistaking the simulation for the real thing if only because users can always look away from the computer screen to remind themselves of the room in which they are sitting. But what about a computer simulation in which users cannot distinguish their real world from the simulated one? What if you looked up in your simulated world, say of the Space Shuttle, and saw the dingy dull ceiling of your office, but the Shuttle's overhead control panel? Proponents of an area of computer development, mostly commonly referred to as virtual reality (VR) hope to achieve the illusion that what appears to be present is not. The interface of a VR system is not the keyboard, not a joystick or a mouse, but your own body. VR blends many areas of interest and inquiry -- computer science, computer visualization, cognitive and perceptual science, even sociology, philosophy, and ethics. As first described in chapter one, one of the best characterizations of VR probably comes from the "holodec" on the television show Star Trek: The Next Generation. However, VR is not science fiction, though the crudeness of the graphics based on current limitations in computer processing power, leaves much to be desired as compared to its sci-fi counterpart. Unlike traditional computer simulations, VR attempts to remove and supplant all competing stimuli with computer-generated stimuli. In order to achieve this, current VR systems make the user wear a helmet containing two video displays, one for each eye, as well as a speaker for each ear. By sending separate visual images to each eye, each offset slightly from the other, the user experiences stereoscopic, or 3-dimensional, vision similar to that of a 3-D movie. The helmet also has sensors to relay information about the user's head movements to the computer. If the user looks right, left, up, or down the computer instructs the video displays to show the corresponding images from the VR world. The user also wears a DataGlove, a special glove with fiber optic sensors that can detect hand movements and relay the signals to the computer. Hence the user moves around the VR through special hand signals, such as pointing the index finger. 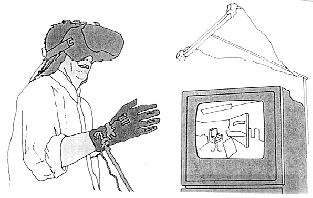 Graphic reprinted with permission of The Computing Teacher. Copyright 1992, International Society for Technology in Education, Eugene, Oregon. The physics of a VR world are determined by the computer program, so it is common for users to fly about or magically go through walls. A VR world might contain "reverse gravity" so that objects fly up to the ceiling when dropped. It is difficult to get a true understanding of VR just from reading about it -- VR must be experienced. I had the opportunity to experience VR, courtesy of Meredith Bricken, a VR scientist at the Human Interface Technology Lab (HITL) at the University of Washington in Seattle. The VR world I visited was unique in that was designed and constructed by children ranging in age from about eight to 16 years old who were participating in a summer technology camp at Seattle's Pacific Science Center. Although the graphics from the video displays were slow (about 10 frames per second) and crude, and the hand movements were awkward, the fact that my visual system was completely dominated by the 3-D graphic display made it surprisingly easy to experience the "out of body" sensation. I felt like I had left the HITL and "entered" the children's VR world. Whether or not virtual reality represent extensions of simulations or microworlds depends largely on how they are used. I still prefer the microworld label to distinguish environments, simulated or otherwise, on the basis of how they allow a user to enter and learn about the world at their level. An example of a VR simulation would be an architectural firm that uses VR to let clients visit and modify a building before it is constructed. However, an example of a VR microworld would be a medical school student learning about sinus cavities in the skull through actually visiting and exploring these recesses. In another sense, virtual reality resembles neither simulations or microworlds. For example, one project being directed by Dr. Michael McGreevy of the NASA/Ames Research Center hopes to physically transport the necessary virtual reality equipment to Mars, so that people can experience Mars without leaving earth. Strictly speaking, this could not be considered a simulation because the visual and tactile stimuli actually are originating from Mars, though the human experience is achieved on Earth (given, of course, the three-second delay to transmit the signal between Mars and Earth). As another example, a surgeon might practice a difficult procedure on a VR model of the patient before performing the real operation. Another prediction is that a surgeon with unique skills in San Francisco could actually perform the operation, VR style, on a real patient with only minutes to live in New York City. Space shuttle astronauts could practice the tricky procedures to share errant satellites before venturing out into space. Tired of putting up with traffic on your way to work in the morning? Then you might like working in a VR office. Although physically you and your office mates are at home, through VR you can "go to work." What are the possibilities of VR for learning and training? If VR developers choose to follow microworld applications, then users must be able to both modify and construct their own VR worlds to match their learning needs (Bricken, 1991). Instead of watching a simulated object fall at varied rates by playing with a gravity setting, users would find themselves falling (although they would also experience some side effects, such as nausea, because the visual system is a more powerful trigger for physical reactions than most people realize -- similar to the feeling one gets simply by watching a video of a roller coaster ride). In a VR microworld, the goal is to achieve the Zen-like sensation of becoming a molecule, a gear, or a neural synapse. In this way, VR microworlds create a sense of empathy between the user the system of interest. For better or worse, the first VR laboratories have only been in tinker mode with the most serious applications so far in the entertainment industry and the military (there is a Nintendo version of the DataGlove). Unfortunately, most of the general public's knowledge of VR has been of its dark side as shown in Stephen King's movie Lawnmower Man. Hopefully, as the cost and limitations of VR decrease, VR can be among the resources that education can casually call upon for environments in which users construct knowledge. |
The degree of realism in a simulation, or the extent to which it resembles the actual experience, is referred to as its fidelity. The assumption that the best simulations are as realistic as possible is a false one. Simply increasing the fidelity of a simulation will not necessarily increase learning (Alessi, 1988). Instead, the relationship between learning and a simulation's fidelity is nonlinear and depends on the instructional level of the student. As shown in Figure 8.1, while it may be appropriate to provide experts with as realistic a simulation as possible, there appears to be optimal levels of fidelity for experienced and especially novice students. In other words, too much realism may cause more harm than good, especially for inexperienced students.
In trying to distinguish between microworlds and simulations, let's start with an example of a microworld that is not a simulation. Cuisenaire rods, a set of colored rods of varying lengths named after George Cuisenaire, the Belgian educator who developed them, act as a microworld for many mathematical ideas (Fuys & Tischler, 1979). Through their manipulation, many young children are introduced to a set of mathematical ideas that are fundamental to learning other, more sophisticated concepts. Despite their simplicity, even the ablest mathematician recognizes them as a mathematical tool. Cuisenaire rods offer mathematics at a level children can understand. On the other hand, Cuisenaire rods offer not a mathematical simulation, but permit real mathematics to take place.
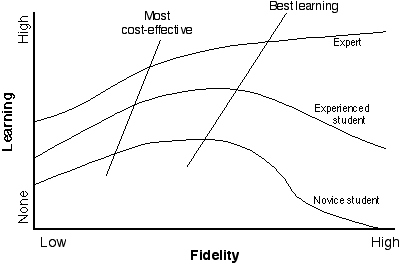
Figure 8.1
The relationship between learning and the fidelity of an instructional simulation on the basis of the experience level of students.
However, simulations can be designed that do not offer any significant difference from real-life experiences, such as sophisticated flight simulators used for training by the military and many major airlines. These simulations would not be considered microworlds for most people because they are designed to represent as many of the variables and factors of the real experience as possible. The simulation is not a microworld because the simulation does not match the user -- the user must match the simulation. The feedback from this simulation would be largely meaningless and nonsensical to all but the most well-trained user.
Simulations start to become microworlds when they are designed to let a novice begin to understand the underlying model. A computer flight simulation can be designed to permit only limited control and manipulation with only one part of the aircraft, such as the rudder. In this sense, the simulation becomes a rudder microworld. Similarly, many microworlds can easily become simulations. Consider a mathematical microworld that involves estimating distances, such as by using the LOGO command FORWARD to move the turtle from one point to another on the screen with as few commands as possible. This microworld becomes a whale search simulation, simply by changing the turtle into an animated boat and the screen target into a whale. The mathematical microworld has not changed, only the context.
Games and Their Relationship to Microworlds and Simulations
Never underestimate the value of play. As adults, we tend to think of play as something that one has to give up when you grow up. However, play serves several cognitive functions in addition to being entertaining and reducing stress. For example, Piaget considered children's play as an assimilation strategy (Piaget, 1951). Through play, one practices a set of information over and over until the individual is completely comfortable and familiar with it. In one sense, play serves as a rehearsal strategy. The knowledge is played over and over in a variety of contexts generated by the individual.
On the other hand, Piaget considered imitation as an accommodation strategy. A child who imitates a parent going off to work by having a doll drive off to the "office" in a toy car with a brief case in the back seat, is reaching out to understand the "go to work" schema. A more detailed account of the value of play is outside the scope of this discussion, but suffice it to say that play is valuable for people of all ages. The instructional computer format of gaming closely parallels educational applications of play. Gaming also offers many similarities to microworlds and simulations, though gaming, too, can remain totally distinctive. The purpose of this section is to consider how to take advantage of gaming techniques in the design of microworlds and simulations.
The value of games is that they are fun. Of course, fun is an extremely abstract concept. One common characteristic of most games is competition, in the form of learner against learner, learner against computer, or learner against self (Hannafin & Peck, 1988). There are many negative aspects to competition, especially those involving learner versus learner. Students who constantly lose may become completely turned off to learning. Yet, there are ways to capture the positive aspects of competition by emphasizing a more enduring characteristic, namely challenge. As first described in chapter 4, Malone (1981) has proposed a framework of intrinsically motivating instruction based on the interplay of three characteristics: challenge, curiosity, and fantasy. In particular, Malone's model has been specifically applied to the design of computer games.
Challenge and curiosity are closely related, and both must be optimally maintained to be effective. Tasks that are too easy can be tedious and boring, and tasks that are too difficult are frustrating and intimidating. In either case, it is unlikely that a student would choose to engage in the activity for even short periods of time. Both challenge and curiosity often result when tasks are novel, moderately complex, or produce uncertain outcomes. An element of surprise results when the expected and actual results for an activity are different. In other words, such events trigger disequilibrium. As previously discussed, completion of challenging tasks can elicit feelings of confidence and competence (Weiner, 1979).
Malone (1981) provides several suggestions for optimizing challenge and curiosity in an educational game:
The element of fantasy is especially important. Fantasy is used to encourage students to imagine that they are completing the activity in a context in which they are really not present. Inducing fantasy relies on mental imagery of contexts that are very meaningful for a student. Fantasy is evident in the intense play of children, especially very young children. Malone (1981) describes two fundamental kinds of fantasies common in the design of computer games: intrinsic fantasies and extrinsic fantasies. As shown in Figure 8.2, the intrinsic or extrinsic nature of the game depends on the degree to which the skill and fantasy are related. Extrinsic fantasies simply overlay some general game context on an existing curriculum area. A common example is the popular "Hang Man" game in which incorrect answers lead to a man being hung, as shown in Figure 8.3. Extrinsic fantasies can re-use the same game design with any content area. There is no mistaking the game elements from the skill or educational value in a game that uses an extrinsic fantasy. In other words, students put up with the skill or educational value given an extrinsic fantasy.
On the other hand, intrinsic fantasies effectively combine or mix the game and skill being learned. The skill and fantasy depend on each other. This means that the skills to be learned are integrated into the fantasy, such as learning about how to use a compass to rescue a party of lost hikers. When effective, the fantasy becomes a meaningful context in which all subsequent instruction can be anchored, or situated (Cognition and Technology Group at Vanderbilt, 1990). Figure 8.4, for example, illustrates an intrinsic fantasy game where players learn about fractions. The game uses the fantasy context of a mine shaft where "some old miner left his ax down in the mine." Players take turns trying to fetch the miner's ax. The mine shafts are meant to convey the concept of a number line. Each player has an elevator that ventures down the mine shaft to a distance equal to the fraction entered. The player who is closest to the ax is rewarded by having the ax loaded into his or her elevator, where it is transported back to the surface and dumped on his or her side. The player with the most axes at the end of the game wins.

Figure 8.2
Games with an intrinsic fantasy have a strong bond between the game's educational value or skill and the game's fantasy whereas in an extrinsic fantasy this relationship is weak.
An interesting element of this game is that there are no wrong answers, just better answers. This helps the players explore the concept of fractions in a nonthreatening way. The game allows for any appropriate fraction and does not require lowest terms. Therefore, a player who enters a fraction like "100/200" will see how it is "related" to the fraction "1/2." As players learn more about fractions, they learn how to tweak fractions, such as entering "499/800" or "501/800" to go just a little before or after "5/8."
Figure 8.5 illustrates an example of an intrinsic fantasy for another version of the "mystery number" game first described in chapter 2. In this version, students try to locate the mystery number with a radar screen. The mystery number is at the center of the radar screen. As the student guesses, the distance away from the center is shown with a blip. Again, errors are a necessary and useful part of this game. Through careful successive guessing, students can pinpoint the identity of the mystery number. The game's fantasy can be extended to a context where the player is trying to help find a lost friend.
Designers are encouraged to provide an intrinsic fantasy in computer games whenever possible. Students who choose to participate in the game are also, therefore, choosing to participate in the instructional skill of the game. The trick, of course, is in finding appropriate intrinsic fantasies that have wide appeal. This recommendation is also extended to the design of microworlds and simulations. In general, the characteristics of intrinsic motivation -- challenge, curiosity, and fantasy -- are also relevant to the design of microworlds and simulations. Gaming contexts provide some of the easiest ways to apply these characteristics.
A final recommendation is made cautiously and with some hesitation. Much can be learned about the design of computer games by how children interact with video games. I dispute the widespread belief that fancy, high-resolution graphics and sound provide the strongest source of motivational appeal of video games. Instead, I contend that the best video games are inherently appealing and enduring because of their attention, accidental or otherwise, to challenge, curiosity, and fantasy. Instructional designers should spend a little more time in video arcades watching and talking to the clientele.
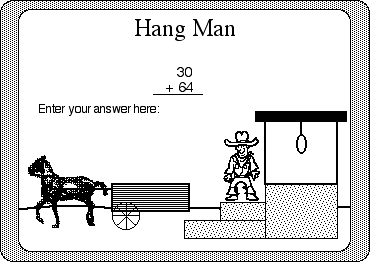
Figure 8.3
An example of an educational game using an extrinsic fantasy. The "hang man" game context is traditional and longstanding and has been used in all subject areas. This particular example uses the context for mathematics. If the student answers correctly, a piece of the "get-away" wagon is added. If the student answers incorrectly, the "desperado" moves one step closer to the "hangman's noose." In an extrinsic fantasy such as this, students who find the game's context enjoyable merely tolerate the educational value. This particular game has other problems, such as the ethical questions of promoting capital punishment and the idea of helping someone escape from their sentence.
In fact, many of the popular video games successfully combine the characteristics of microworlds in the gaming. Figures 8.6 and 8.7 show two simple examples of how this combination might be accomplished in designing highly interactive programs for young children or the learning-disabled. Figure 8.6 could be viewed as a "left hand versus right hand" microworld in the intrinsic game context of a treasure hunt. Figure 8.7 is a "1, 2, 3" microworld for learners to explore these simple, yet crucial principles from number theory.
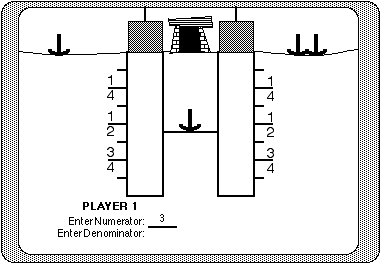
Figure 8.4
An example of an educational game using an intrinsic fantasy. The content of the game, fractions, is closely related to the fantasy of a mine shaft. Students play this game in pairs. Each tries to lower their "elevator" to the exact location of the miner's ax. Using animation, the elevator demonstrates the idea of fractions on a number line by dropping the elevator down from 0 (the surface) to the fraction chosen by each of the players. The ax gets loaded into the player's elevator that is closest to the "lost ax." Both elevators are "pulled" back up to the surface and the ax is "dumped" on to the winning player's side of the mine. The player with the most axes at the end of the game wins.
Space Shuttle Commander: Practical Constructivism
All of my trials, tribulations, and adventures in instructional technology have been a result of my own personal "disequilibrium" in my attempting to understand and apply many interpretations of the field. Interestingly, I began my career as a classroom teacher about the same time that microcomputers were invented. My training as a teacher was rooted in the Piagetian approach, yet I found it hard to translate theory into practice, given all of the typical constraints inherent in the public school classroom. But rather than give in to the frustration, I, too, adapted (i.e., assimilated and accommodated) by instituting a pattern of compromise between philosophical and practical circumstances. As a result, my view of instructional technology is an eclectic one.
As a case in point, the next section will describe my attempt at developing a software package, Space Shuttle Commander (SSC), that is meant to act as a prototype or model of how one might merge instructivist and constructivist goals and philosophies (Rieber, 1990c, 1992). The next section will provide an overview of SSC, followed by a set of design recommendations that helped guide its development. As you will see, computer graphics have been my main arsenal for realizing the blending of constructivist and instructivist goals in the design of interactive activities. Another way of looking at this approach is simply to blend the best ideas behind the design of microworlds, simulations, and games.
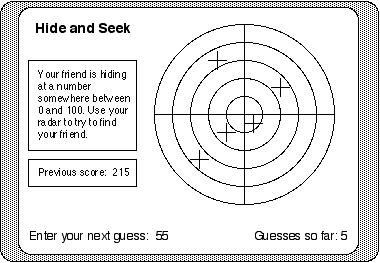
Figure 8.5
Another example of an educational game using an intrinsic fantasy. In this example, number theory and estimation skills are intertwined with the game's fantasy. In this example, the goal is to find a friend who is hiding at a number randomly chosen by the computer. Guesses show up as blips on the radar screen. The closer the blips are to the cross-hairs at the center of the radar, the better the guess. Students use the feedback from their guesses to triangulate, or pinpoint, the identity of the random number and, in so doing, find their friend.
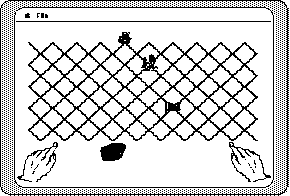
Figure 8.6
An example of combining the characteristics of microworlds and games to learn the simple directions of left and right. The student uses the mouse to click on either hand, followed by the computer saying "left" or "right" and the boat animated in the corresponding direction.
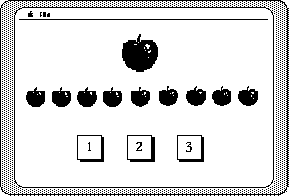
Figure 8.7
Another example of combining the characteristics of microworlds and games to learn the mathematical concepts of 1, 2, and 3. The student uses the mouse to click on one of the numbers and the computer, through animation, "eats" the corresponding number of apples. The goal is to eat all the apples.
An Overview of Space Shuttle Commander
SSC is designed for elementary and middle school students. The purpose of SSC is to help these students achieve a wide range of learning goals related to Newton's laws of motion. SSC was designed based on compromises between the extreme views of both instructivism and constructivism. For example, SSC accepts the constructivist position that learners should be given rich and powerful environments to build and transform mental structures. However, SSC also acknowledges the practicality of the current educational system, though this may be regarded as a necessary evil at the present.
SSC is a direct application of a physics microworld first designed by Andy diSessa (1982) involving a screen object called a dynaturtle. The dynaturtle closely resembles the more familiar LOGO turtle described in chapter 3, except that it has one more characteristic -- velocity. By manipulating the dynaturtle, students can explore motion principles in a simulated frictionless, gravity-free environment. In SSC, the dynaturtle microworld becomes a simulation by placing it in the context of space travel. The dynaturtle becomes a "space shuttle" and students are encouraged to fantasize they are astronauts.
SSC tries to use both tutorials and simulation/gaming (called "flight lessons" and "missions," respectively) in ways that maximize their strengths and minimize their weaknesses. For example, a tutorial is a good way to present large amounts of information in an organized way. However, tutorials are often dull and prone to promoting passive learning (cf. Merrill, Li, & Jones, 1990a; Jonassen, 1988b; Roblyer, 1988). Simulations and games are usually much more motivating and are well suited to discovery learning, though learning can be difficult to monitor and assess (Alessi & Trollip, 1985, 1991; Hannafin & Peck, 1988). Both the flight lessons and missions introduce students to the laws of motion in nonmathematical ways. The flight lessons present and explain the concepts in a structured, step-by-step way. The missions offer students a series of simulations, most with game-like features. Students pilot an animated shuttle, such as that represented in Figure 8.8.
Traditional instructional design usually promotes deductive learning strategies, such as presenting a concept to students followed by an assortment of examples and nonexamples and by practice (R. Gagné, 1985; Gagné, Briggs, & Wager, 1992). Constructivists, in contrast, promote interaction over explanation. Students are expected to discover, or induce, concepts and principles on their own based on experience and interpretation. Bruner (1986) referred to these inductive learning experiences as learning by inventing (p. 127).
The activities in SSC can be used for deductive or inductive approaches. Students can go through SSC in a deductive fashion simply by following the course structure, represented in Figure 8.9, starting with the first flight lesson. This approach takes full advantage of the learning hierarchy designed into SSC, where later skills build on those introduced earlier (Dunn, 1984; R. Gagné, 1985). Each flight lesson "teaches" the respective objectives according to conventional instructional design, and each "mission" acts as a suitable practice activity for each lesson.
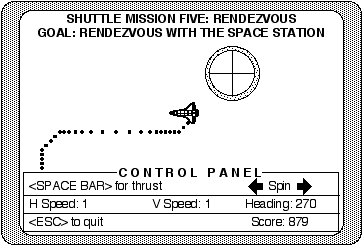
Figure 8.8
A representation of the computer screen during an episode of "Mission 5: Rendezvous." The animated shuttle is under student control. Arrow keys rotate the shuttle in 90 degree increments and the space bar gives the shuttle a "kick" or thrust in the direction it is pointing. The goal of this mission is to maneuver the shuttle to the space station.
On the other hand, each mission acts as a stand-alone microworld. Each mission simulates particular aspects of Newton's laws of motion. Early missions are very structured, with the number of learning variables minimized to help make fundamental ideas and concepts as explicit for students as possible. Later missions are very open-ended, but with the option of imposing or reducing structure and complexity. It is possible to have students begin to understand Newtonian mechanics by having them only explore the missions in SSC. Flight lessons would be consulted as additional resources, either as the result of curiosity or confusion.
It is expected that educators would use SSC depending on the philosophical orientation they hold. For example, an instructivist would probably focus on the flight lessons and only consider the missions as practice activities. On the other hand, a constructivist would probably only see value in the missions (and may even object to the presence of the flight lessons). A constructivist would let the learner determine sequence, whereas an instructivist would encourage or require the learner to closely follow SSC's course map. SSC affords a wide range of interpretations, by both teachers and students, on how it should be used.
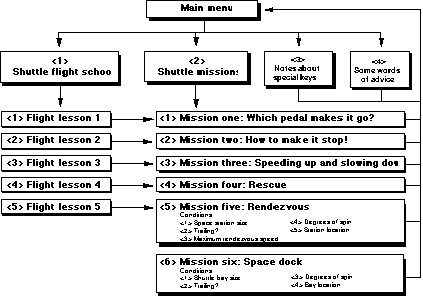
Figure 8.9
A course flowchart of Space Shuttle Commander.
Another instructivist influence is on the overall design of the series of missions. The missions are hierarchically organized from simple to complex -- early missions focus on the simplest ideas, and later missions combine and extend these ideas. For example, missions 1, 2, and 3 take the learner through a series of activities that introduce the simplest aspects of Newton's first and second laws. At first, structure is heavily imposed, but it is reduced as the learner establishes a foothold with these concepts. The first three missions further constrain the learner's experience to one dimension, as shown in Figure 8.10. However, mission 4, as illustrated in Figure 8.11, introduces the effects of two dimensions in a highly structured way so as to make the simplest relationships of two-dimensional motion as explicit as possible. This is accomplished by placing artificial restraints on the microworld. The student is told that the shuttle has been in a collision with a small asteroid, resulting in several malfunctions. For example, the student has no control over steering and must contend with the fact that the shuttle is pointing directly to the right (i.e., 90-degree heading). The shuttle is also coasting in space toward the 0-degree heading (i.e., from bottom to top), and the student only has enough fuel left for three maneuvers. The goal of the mission is for the student to "rescue" the shuttle by using the limited resources to fly the shuttle to the space station located, fortunately, nearby.
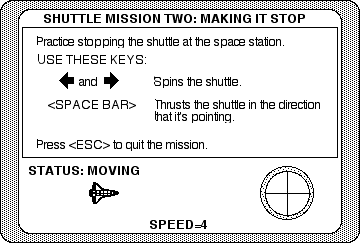
Figure 8.10
A representation of the computer during "Mission 2: Making It Stop." By programming the computer to constrain the "spin" to 180 degree increments, the shuttle is confined to one dimension. This makes it easier for the learner to explore and focus on the idea of how forces act on the shuttle's speed and direction.
The final two missions, "Rendezvous," (see Figure 8.8) and "Space Dock" (see Figure 8.12), are highly detailed simulations. Students who unsuccessfully attempt these final two missions early on are encouraged by on-line coaching (and perhaps by the teacher) to go through earlier missions or flight lessons. Such use of coaching is a recognized instructivist strategy. Of course, constructivists would expect many students to discover much about Newton's laws of motion just by their experiences with these two missions.
A clear and simple goal is made overt to each student in each mission. The goal provides a simple tool for students to evaluate their interaction during the mission. All of the continuous feedback received from the microworld -- the motion of the shuttle, the trail left by the shuttle, and the verbal information from the control panel -- can be used to compare the shuttle's current state against the desired state (i.e., the goal). For example, the goal from mission 5, as shown in Figure 8.8, is "fly the shuttle to the space station." Besides its use as a game characteristic, successful completion of the goal also provides a means for teachers to evaluate performance across a group of students, similar to the use of performance objectives in most instructivist models.
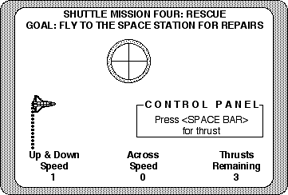
Figure 8.11
A representation of the computer screen during "Mission 4: Rescue." The goal of the mission is to maneuver a "disabled" shuttle to the space station. Students do not have control over the shuttle's rotation, and they only have enough fuel for three bursts of thrust. These constraints make the relationship of orthogonal forces (those occurring in 90 degree increments) more apparent.
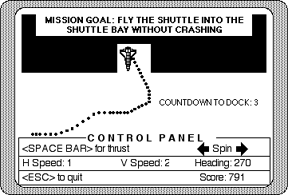
Figure 8.12
A representation of the computer screen during "Mission 5: Space Dock." The goal of this mission is to maneuver the shuttle to the shuttle "bay" of the space station without touching the walls of the bay or the station. This mission, even in its simplest form, is considerably more difficult than all of the other missions.
Graphics support many aspects of SSC. They induce the fantasy of piloting the space shuttle and also help explain the scientific concepts and principles. Perhaps most important, graphics are used as a critical source of continuous feedback to learners as they complete the missions. Compare, for example, Figure 8.8 with Figure 8.13, a hypothetical example where all of the graphics are replaced with pure verbal information. All of the raw information given to the learner is the same in both cases, yet the differences are stark and obvious. This intuitive graphical feedback is a natural mapping between the physics of SSC and the user.
Instructional Design Recommendations Rooted in Constructivism
Table 8.2 summarizes a series of considerations that guided the design and development of SSC. These guidelines have both instructivist and constructivist influences and, as such, are offered as a working compromise between these learning philosophies. However, more important, these guidelines also offer a means of understanding and incorporating constructivist goals in instruction. These guidelines are meant to complement the fourteen design recommendations discussed in chapter 7.
| Table 8.2 Some considerations in the design of interactive learning environments based on characteristics of microworlds, simulations, and games |
|
Reprinted from Rieber, L.P. (1992). Computer-based microworlds: A bridge between constructivism and direct instruction. Educational Technology Research and Development, 40(1), 93-106. Copyright 1992 by the Association for Educational Communications and Technology. Reprinted by permission of the publisher.
1. "Provide a meaningful learning context that supports intrinsically motivating and self-regulated learning" (Rieber, 1992, p. 98). For learning to be a meaningful experience, it must directly connect to the learner's life in some way. The best examples of meaningful learning are anchored in contexts that are relevant and interesting for learners (Cognition and Technology Group at Vanderbilt, 1990, 1992). My experience has been that children and adults find it easy and fun to imagine they are astronauts. The context of space travel lends itself very well to both real-life drama and science fiction. In SSC, students are not watching someone else's experience in space, such as a video documentary about space travel. Instead, they can take their own imaginary trip aboard the shuttle through realistic fantasy. Students are not just along for the ride, they are in control.
The purpose of the missions is to induce and encourage the fantasy while helping the student to build awareness and competency in many science concepts and principles in a series of structured activities. Research shows initial evidence that the SSC missions hold intrinsically motivating appeal for elementary school children (Rieber, 1991b). Another example (and more widespread) of using a meaningful context for learning is the Voyage of the Mimi, a math and science curriculum set in the context of whale exploration (Bank Street College of Education, 1989; a sequel is based on Mayan archaeology).
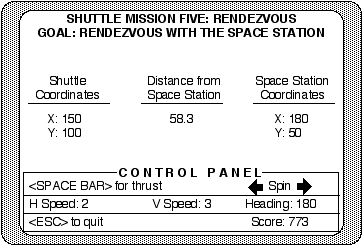
Figure 8.13
A hypothetical example of designing "Mission 5: Rendezvous" without the use of the graphical, animated feedback. This screen presents all of the same information presented in Figure 8.5, but in all verbal form. In order to interpret this feedback, the learner would have to mentally construct the corresponding visual elements.
Malone (1981) concludes that an activity needs to continually challenge students in order to maintain its intrinsic appeal. Several of the SSC missions, for example, provide students with the opportunity to vary the "mission conditions" (such as target size, target location, and shuttle rotation) in order to increase the difficulty of the activity, as shown in Figure 8.14. For example, it is much simpler to control the shuttle in two-dimensional space when the shuttle's rotation is kept to 90-degree increments. Control of the shuttle becomes much more difficult when control is changed to 45- or 30-degree increments. Scorekeeping features, another feature noted by Malone (1981) as a way to increase intrinsic appeal in computer games, also are provided.

Figure 8.12
Sample screen showing the various mission "conditions" of Rendezvous that can be changed to increase the difficulty of the mission. A similar set of mission conditions is available for "Mission 5: Space Dock."
2. "Establish a pattern where the learner goes from the "known to the unknown" (Rieber, 1992, p. 100). Although research continually shows the importance of the learning context, meaningfulness can also be interpreted as the degree to which students can link new ideas to what they already know. In fact, the strength of the relationship between new information and prior knowledge may be among the most important determinants of learning (Ausubel, 1968). Many learning theorists have offered strategies for maximizing this relationship. Bruner (1966), for example, suggests a spiral approach where the simplest and most general ideas are introduced first to learners in highly interactive and concrete ways. These ideas are then reintroduced to students over and over at increasing levels of abstraction and detail. Similar models have been promoted where the most general ideas grasped early by learners are critical in helping them to comprehend much more detailed ideas introduced later (Ausubel, 1963; Reigeluth & Stein, 1983).
SSC tries to provide students with a strong conceptual understanding of Newtonian principles in order to act as "anchoring posts" for later instruction. SSC can help bridge the learning of formal physics as it is usually taught in schools with the experiential learning of the dynaturtle. Paradoxically, traditional physics instruction usually tries to simplify learning by conveniently removing the influences of friction and gravity from the mathematical equations. Unfortunately, life without fraction and gravity is outside the experience of virtually every student. SSC can give students these experiences in a simulated context. The simulated space shuttle, like its cousin the dynaturtle, acts as a transitional object between the learner and Newtonian physics, thereby acting as an "object to think with" -- a characteristic of microworlds discussed earlier.
3. "Provide a balance between deductive and inductive learning" (Rieber, 1992, p. 101). Obviously, learning entails and requires both deductive and inductive approaches. An inexperienced homeowner may fix a leaky faucet by getting involved in the project outright or by consulting and carefully following a "how to" book. Extreme interpretations of either a deductive or inductive approach are obvious. Strict deductive approaches are prone to assigning a passive role to the learner. Instructional designs based on cookbook strategies usually lack both imagination and innovation. Lesson activities begin to resemble one another. Deductive approaches are much easier to apply for lower-level learning outcomes, such as fact learning, because there is little need for interpretation or "construction" on the part of the learner. On the other hand, strict inductive approaches are based on a "sink-or-swim" philosophy. Learners are at risk of becoming either frustrated or bored if they are unsuccessful or disinterested early on. Novices to a domain or content may also need structure or guidance that purely inductive experiences do not provide. Designers of hypertext, for example, report that novice learners are often prone to disorientation (Jonassen, 1986; Tripp & Roby, 1990). Inductive activities also require a playful attitude and a willingness to go exploring, conditions that older children and adults may resist (Seaman & Fellenz, 1989). The most successful learning environments carefully combine the strengths of direct instructional methods with some level of personal discovery and exploration (Sfondilias & Siegel, 1990). Though balancing deductive and inductive learning is not a simple task, it is an achievable and worthwhile goal and was inherent in the design of SSC.
4. "Emphasize the usefulness of errors" (Rieber, 1992, p. 101). What are your memories of learning in school? For many people, it was a time of simply trying to find out the right answer while trying to avoid getting the wrong answer. Too much of a student's job is in just figuring out what the teacher already knows. Errors imply failure. This is unfortunate. Most of the learning in life that really counts is not only in discovering things that are totally new and original, but are also all at once challenging and complex. Rather than destructive, errors are essential for learning and are among the most instructive sources of information when an individual is engaged in problem solving (Fredericksen, 1984; Schimmel, 1988). Inductive learning theories promote the ability of learners to detect errors and then incorporate the information learned in subsequent trials. Error handling is a systematic process usually referred to as debugging in computer applications. Some of the most fundamental learning, such as concept formation, requires a student to isolate and control one or more variables while holding all other variables constant (see Mayer, 1983, for a review). In this way, a learner performs a series of "mini-experiments" to test a hypothesis. An example is someone installing a new light fixture who must first determine which breaker controls the electricity to that part of the house. A person's hypothesis testing may include the strategy of turning on lights or appliances throughout the house to see which lose power when each breaker is tripped in isolation.
Unfortunately, many learning tasks contain so many individual variables that a novice would soon be inundated with information and become frustrated, such as learning how to use a new software package given only a cryptic reference manual. Microworlds offer a way to structure a learning experience so that only a limited number of variables are introduced at a given time in a context that is relevant and meaningful. This is sometimes referred to as the project approach. For example, it might help someone learning a word processor for the first time if a project with constrained boundaries are given, but with real and meaningful goals, such as writing a letter to a friend. When initial skills are mastered (such as entering, correcting, and saving text), additional variables can be introduced (such as how to underline, center, or print). In many physics problems, such as classical mechanics, problems are simplified when set in the context of one rather than two dimensions. The microworld of the SSC missions accomplishes this by turning on or off certain computer commands, depending on the mission. Some of the missions limit the rotation of the shuttle to 180 degrees, resulting in one-dimensional motion. Other missions begin by having the user rotate the shuttle in 90-degree increments, though the user can change this later if desired. This assures that the user first experiences how to maneuver the shuttle in two dimensions with the simplest case.
For errors to be useful, the goal of an activity must be clearly known to learners (Norman, 1988). If the goal is ambiguous, then all available feedback will be ambiguous as well. Again, the project approach is a useful strategy. In LOGO, for example, students often work toward completing a graphic they have designed beforehand, such as a house or a car. All of the graphical feedback given to them by the turtle is continually judged against their predetermined goals. This is referred to as goal monitoring, which, in the best of cases, is automatic and intrinsic (Schunk, 1990). The best advice is to provide the simplest and clearest goals when designing microworlds. Common examples of mission goals in SSC are "make the shuttle come to a stop" or "fly the shuttle to the space station."
Errors are one important type of feedback that can take many forms, such as graphical, verbal, tactile, and aural. A variety of feedback types can also be used within a microworld so long as it all helps a learner to be successful in hypothesis forming and testing. For example, the user can choose to have the shuttle in SSC leave a trail as it moves. Verbal feedback, such as the information about the shuttle's speed, position, and heading, can also be presented along with the visual feedback. This kind of verbal feedback can be particularly helpful when students have difficulty seeing slight visual changes to the shuttle's speed or direction.
5. "Anticipate and nurture incidental learning" (Rieber, 1992, p. 102). Constructivists recognize that learning rarely follows a fixed sequence that is the same for all learners. Indeed, some of the most worthwhile learning will not be anticipated. History is full of examples of scientific discoveries and technological innovations that are the result of creative insight and unplanned tinkering. The trick is not only being in the right place at the right time, but also recognizing when one is confronted with a unique opportunity. In LOGO programming, for example, mistakes and other unintended or unexpected events often lead to interesting visual effects. Students often choose to revise (or abandon) the original programming project to pursue the unexpected results. Of course, it can be difficult to identify and document achievement in terms of unanticipated learning goals or competencies. There is also the risk that incidental learning will be irrelevant and trivial.
Instructivist approaches, on the other hand, try to take a group of learners through an instructional sequence designed to meet predetermined learning objectives. Learners are actually discouraged from exploring anything incidental to these objectives. Carefully designed microworlds help to balance the risks and incentives associated with both intentional and incidental learning. Incidental learning is expected and hoped to occur, but within design parameters. The teacher plays a critical role here. There is a need to channel incidental learning back toward the lesson objectives or to revise lesson objectives to accept unexpected learning outcomes. Of course, students who become sidetracked in unproductive ways should be redirected back to a relevant path. The teacher needs to act as the "safety valve" to make sure that a learner's actions are not counterproductive without thwarting or quelling potentially worthwhile incidental learning activities.
One of the studies discussed in chapter 6 (i.e., Rieber, 1991b) aptly shows both the potentials and risks of incidental learning. Recall that fourth-grade students successfully extracted incidental information about Newton's second law from an animated display, but also inappropriately applied this information to other contexts involving the law of gravity. Incidental learning must be carefully monitored and assessed so that it remains constructive and applicable to at least the broadest set of learning goals without contributing to misconceptions.
REVIEW
